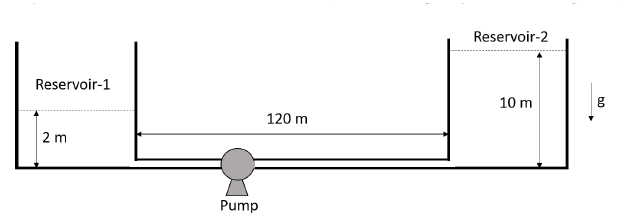
Two reservoirs located at the same altitude are connected by a straight horizontal pipe of length $120\:m$ and inner diameter $0.5\:m$, as shown in the figure. A pump transfers the liquid of density $800\:kg\:m^{-3}$ at a flow rate of $1\:m^{3}\:s^{-1}$ from Reservoir-$1$ to Reservoir-$2$. The liquid levels in Reservoir-$1$ and Reservoir-$2$ are $2\:m$ and $10\:m$, respectively. Assume that the reservoirs’ cross-section areas are large enough to neglect the liquid velocity at the top of the reservoirs. All minor losses can be ignored. The acceleration due to gravity is $9.8\:ms^{-2}$. If the friction factor for the pipe-flow is $0.01$, the required power of the pump is _________________ $\text{kW}$ (rounded off to one decimal place).