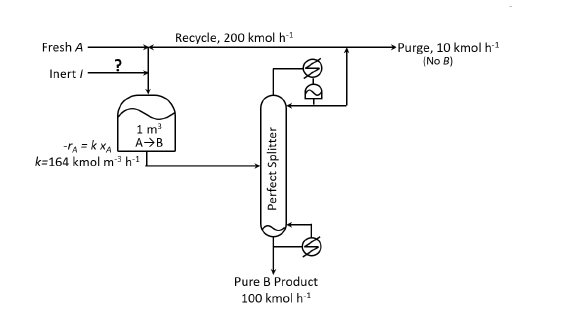
Consider the process flowsheet in the figure. An irreversible liquid-phase reaction $A \rightarrow B$ (reaction rate $-r_{A} = 164 \:x_{A}\text{ kmol }m^{-3}\:h^{-1}$) occurs in a $1\:m^{3}$ continuous stirred tank reactor $\text{(CSTR)}$, where $x_{A}$ is the mole fraction of $A$. A small amount of inert, $I$, is added to the reactor. The reactor effluent is separated in a perfect splitter to recover pure $B$ product down the bottoms and a $B$-tree distillate. A fraction of the distillate is purged and the rest is recycled back to the reactor. At a particular steady state, the product rate is $100\text{ kmol }h^{-1}$, the recycle rate is $200\text{ kmol }h^{-1}$ and the purge rate is $10$ kmol $h^{-1}$. Given the above information, the inert feed rate into the process is _______________ $\text{ kmol }h^{-1}$ (rounded off to two decimal places).