A U-tube manometer contains two manometric fluids of densities $1000 \: kg \: m^{-3}$ and $600 \: kg \: m^{-3}$. When both the limbs are open to atmosphere, the difference between the two levels is $10 \: cm$ at equilibrium, as shown in the figure.
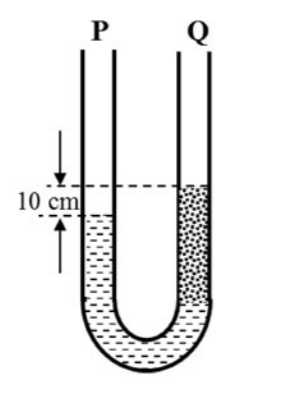
The rest of the manometer is filled with air of negligible density. The acceleration due to gravity is $9.81 \: m \: s^{-2}$ and the atmospheric pressure is $100 \: kPa$. How much absolute pressure (in $kPa$) has to be applied on the limb $’P’$ to raise the fluid in the limb $’Q’$ by another $20 \: cm$?
- $100.175$
- $103.924$
- $547.231$
- $833.206$