A student performs a flow experiment with Bingham Plastic under fully developed laminar flow conditions in a tube of radius $0.01 \: m$ with a pressure drop $(\Delta P)$ of $10 \: kPa$ over tube length $(L)$ of $1.0 \: m$. The velocity profile is flat for $r<r_c$ and parabolic for $r \geq r_c$, as shown in the figure.
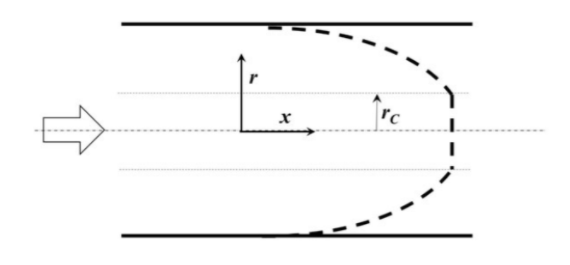
Consider $r$ and $x$ as the radial and axial directions, and the shear stress is finite as $r$ approaches zero. A force balance results in the following equation $$\dfrac{d(r \tau _{rx})}{dr} = r \dfrac{(-\Delta P)}{L}$$ where $\tau_{rx}$ is the shear stress. If $r_c$ is $0.001 \: m$, then the magnitude of yield stress for this Bingham Plastic (in $Pa$) is
- $1$
- $5$
- $8$
- $12$