Let the side of a cube be $a\;\text{cm}.$
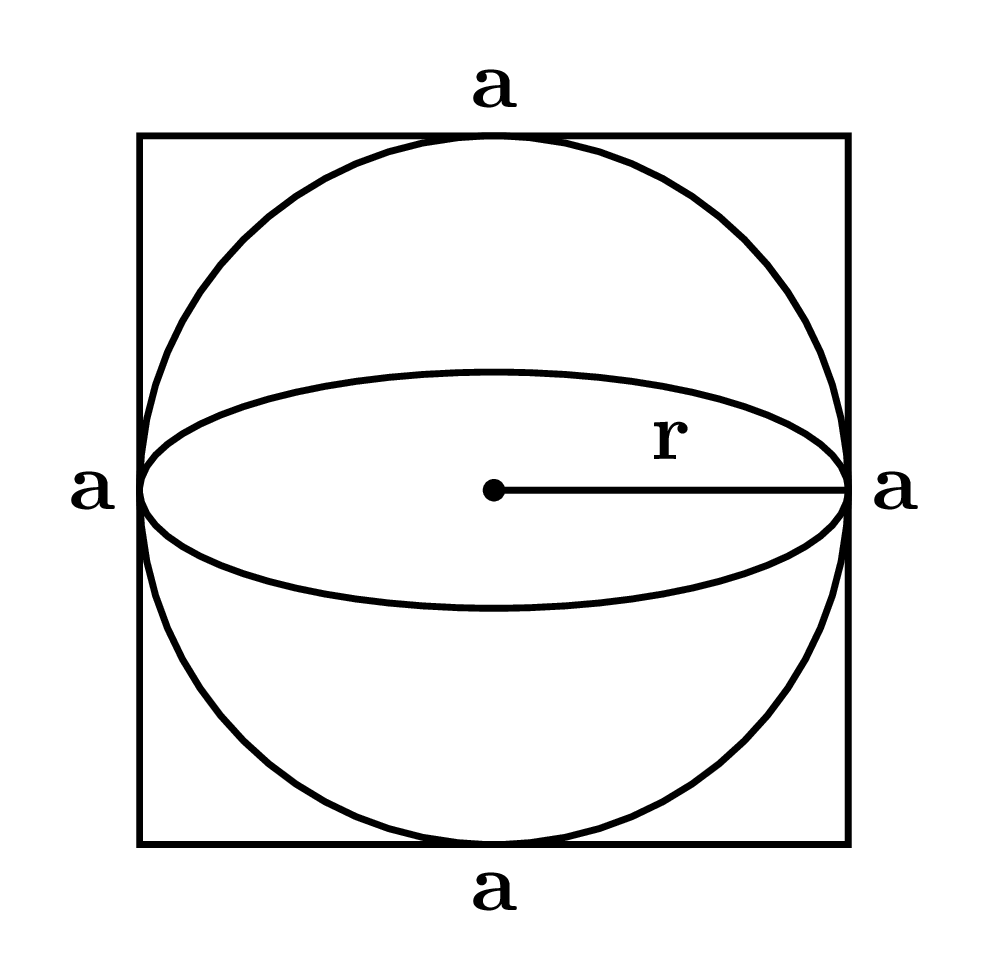
The diameter of a sphere is equal to the side of a cube.
$\Rightarrow \boxed{a = 2r}$
$\therefore$ The volume of a box of the cubical shape $ = a^{3} = (2r)^{3} = 8r^{3} \;\text{cm}^{3}.$
Correct Answer $:\text{D}$