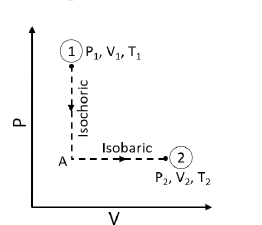
$N$ moles of an ideal gas undergo a two-step process as shown in the figure. Let $\text{P, V and T}$ denote the pressure, volume and temperature of the gas, respectively. The gas, initially at state-$1$ $(P_{1}, V_{1},T_{1})$, undergoes an isochoric (constant volume) process to reach state-$A$, and then undergoes an isobaric(constant pressure) expansion to reach state-$2$ $(P_{2},V_{2},T_{2})$. For an ideal gas, $C_{P} - C_{V} = NR$, where $C_{P}$ and $C_{V}$ are the heat capacities at constant pressure and constant volume, respectively, and assumed to be temperature independent. The heat gained by the gas in the two-step process is given $\text{bv}$
- $P_{2}\left ( V_{2} - V_{1}\right ) + C_{v}\left ( T_{2} - T_{1}\right )$
- $P_{2}\left ( V_{2} - V_{1}\right ) + C_{P}\left ( T_{2} - T_{1}\right )$
- $C_{P}\left ( T_{2} - T_{1}\right ) + C_{V}\left ( T_{2} - T_{1}\right )$
- $P_{2}V_{2} - P_{1}V_{1}$