Two ideal cross-current stages operate to extract $P$ from a feed containing $P$ and $Q$, as shown below.
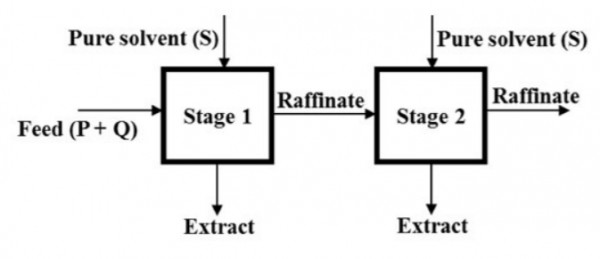
The mass flow rates of $P$ and $Q$ fed to Stage $1$ are $1,000 \: kg h^{-1}$ and $10,000 \: kg \: h^{-1}$, respectively. Pure solvent $(S)$ is injected at mass flow rates of $5,000 \: kg \: h^{-1}$ and $15,000 \: kg \: h^{-1}$ to Stages $1$ and $2$ respectively. The components $Q$ and $S$ are immiscible. The equilibrium relation is given by $Y^* =1.5X$, where $X$ is the mass of $P$ per unit mass of $Q$ in the raffinate and $Y^*$ is the mass of $P$ per unit mass of $S$ in the extract, which is in equilibrium with the raffinate. The mass flow rate of $P$ (in $kg \: h^{-1}$) in the raffinate from Stage $2$ is ________ (round off to nearest integer)