For a unit step input, the response of a second order system is
$$y\left ( t \right )=K_{p} \left [ 1-\frac{1}{\sqrt{1-\zeta ^{2}}} e^{\frac{\zeta t}{\tau }}\sin\left ( \frac{\sqrt{1-\zeta ^{2}}}{\tau } t+\phi \right ) \right ]$$
where, $K_{p}$ is the steady state gain, $\zeta$ is the damping coefficient, $\tau$ is the natural period of oscillation and $\phi$ is the phase lag. The overshoot of the system is $exp \left ( -\frac{\pi \zeta }{\sqrt{1-\zeta ^{2}}} \right )$. For a unit step input, the response of the system from an initial steady state condition at $t=0$ is shown in the figure below.
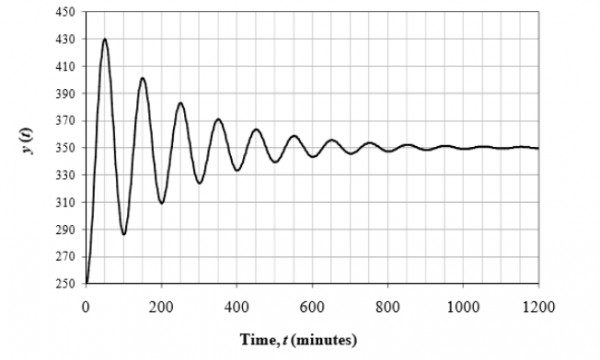
What is the natural period of oscillation (in seconds) of the system?
- $15.9$
- $50$
- $63.2$
- $100$