Consider the process in the figure. The liquid phase elementary reactions $$A + B \rightarrow P \:\:\:\: -r_{B1} = k_{1}\:x_{A}\:x_{B}$$ $$P + B \rightarrow S \:\:\:\: -r_{B2} = k_{2}\:x_{P}\:x_{B}$$ $$S + A \rightarrow 2P \:\:\:\: -r_{S3} = k_{3}\:x_{S}\:x_{A}$$ occur in the continuous stirred tank reactor $\text{(CSTR)}$, where $x_j$ is the mole fraction of the $j^{th}$ component $\text{(j = A,B, P, S)}$ in the $\text{CSTR}$. It is given that $k_{2} = k_{3}$. All process feed, process exit and recycle streams are pure. At steady state, the net generation rate of the undesired product, $S$, in the $\text{CSTR}$ is zero. As $q= x_{A}/x_{B}$
is varied at constant reactor temperature, the reactor volume is adjusted to maintain a constant single-pass conversion of $B$. For a fixed product rate and $90\%$ conversion of $B$ in the reactor, the value of $q$ that minimizes the sum ot the molar flow rates of the $A$ and $S$ recycle streams is ________________ (rounded oft to one decimal place).
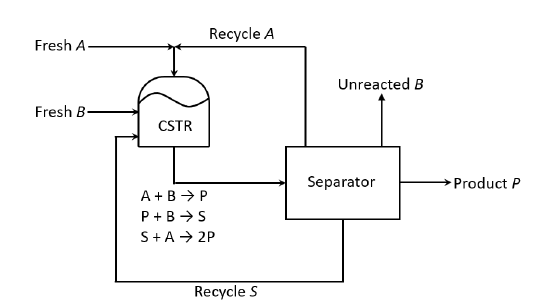
All fresh feeds, process exit streams and recycle streams are pure