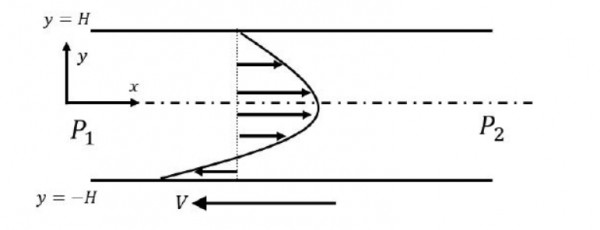
Consider a steady, fully-developed, uni-directional laminar flow of an incompressible Newtonian fluid (viscosity $\mu$ ) between two infinitely long horizontal plates separated by a distance $2 \mathrm{H}$ as shown in the figure. The flow is driven by the combined action of a pressure gradient and the motion of the bottom plate at $y=-H$ in the negative $x$ direction. Given that $\frac{\Delta P}{L}=\frac{\left(P_{1}-P_{2}\right)}{L}>0$, where $P_{1}$ and $P_{2}$ are the pressures at two $x$ locations separated by a distance $L$. The bottom plate has a velocity of magnitude $V$ with respect to the stationary top plate at $y=H$. Which one of the following represents the $x$-component of the fluid velocity vector?
- $\frac{\Delta P}{L} \frac{H^{2}}{2 \mu}\left(1-\frac{y^{2}}{H^{2}}\right)+\frac{V}{2}\left(\frac{y}{H}-1\right)$
- $\frac{\Delta P}{L} \frac{H^{2}}{2 \mu}\left(\frac{y^{2}}{H^{2}}-1\right)+\frac{V}{2}\left(\frac{y}{H}-1\right)$
- $\frac{\Delta P}{L} \frac{H^{2}}{2 \mu}\left(\frac{y^{2}}{H^{2}}-1\right)-\frac{V}{2}\left(\frac{y}{H}-1\right)$
- $\frac{\Delta P}{L} \frac{H^{2}}{2 \mu}\left(1-\frac{y^{2}}{H^{2}}\right)-\frac{V}{2}\left(\frac{y}{H}-1\right)$