Consider an infinitely long rectangular fin exposed to a surrounding fluid at a constant temperature $T_a=27^{\circ}C$.
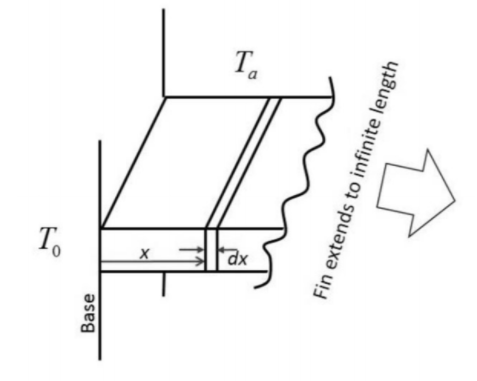
The steady state one dimensional energy balance on an element of the fin of thickness $dx$ at a distance $x$ from its base yields $$\dfrac{d^2\theta}{dx^2} = m^2 \theta$$ where $\theta = T_x-T_a, \: T_x$ is the temperature of the fin at the distance $x$ from its base in $^{\circ}C$. The value of $m$ is $0.04 \: cm^{-1}$ and the temperature at the base is $T_0=227^{\circ}C$. The temperature (in $^{\circ}C$) at $x=25 \: cm$ is __________ (round off to $1$ decimal place).