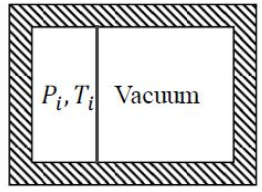
Consider a rigid, perfectly insulated, container partitioned into two unequal parts by a thin membrane (see figure). One part contains one mole of an ideal gas at pressure $P_{i}$ and temperature $T_{i}$ while the other part is evacuated. The membrane ruptures, the gas fills the entire volume and the equilibrium pressure is $P_{f}=P_{i}/4$. If $C_{p}$ (molar specific heat capacity at constant pressure), $C_{v}$ (molar specific heat capacity at constant volume) and $R$ (universal gas constant) have the same units as molar entropy, the change in molar entropy $\left ( S_{f} -S_{i}\right )$ is
- $C_{p}$In$2$ +$R$In$4$
- $-C_{v}$In$2$ +$R$In$4$
- $R$In$4$
- $C_{p}$In$2$