A person is drowning in sea at location $R$ and the lifeguard is standing at location $P$. The beach boundary is straight and horizontal, as shown in the figure.
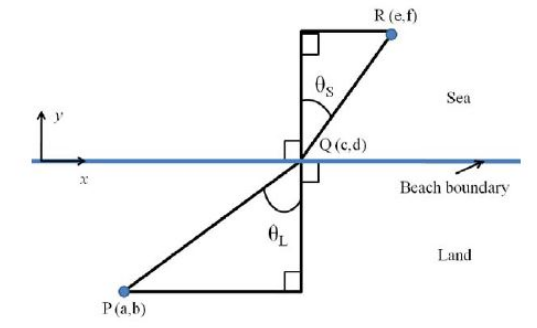
The lifeguard runs at a speed of $V_{L}$ and swims at a speed of $V_{s}$. In order to reach to the drowning person in optimum time , the lifeguard should choose point $Q$ such that
- $\frac{sin^{2}\Theta _{L}}{sin^{2}\Theta _{S}}=\frac{V_{S}}{V_{L}}$
- $\frac{sin\Theta _{L}}{sin\Theta _{S}}=\frac{V_{S}}{V_{L}}$
- $\frac{sin^{2}\Theta _{L}}{sin^{2}\Theta _{S}}=\frac{V_{L}}{V_{S}}$
- $\frac{sin\Theta _{L}}{sin\Theta _{S}}=\frac{V_{L}}{V_{S}}$