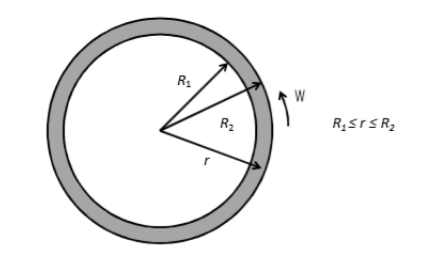
An incompressible Newtonian fluid , filled in an angular gap between two concentric cylinders of radii $R_{1}$ and $R_{2}$ as shown in the figure, is flowing under steady state conditions. The outer cylinder is rotating with an angular velocity of $\Omega$ while the inner cylinder is stationary. Given that (R$_{2}$ – R$_{1}$) $\ll$ R$_{1}$, the profile of the profile of the $\theta$-component of the velocity V${_\theta}$ can be approximated by,
- $R{_2}\Omega$
- $\frac{(r – R{_2})}{(R{_2} – R{_1})}$r$\Omega$
- $\frac{(r + R{_1})}{(R{_2} + R{_1})}$R${_1}$$\Omega$
- $\frac{(r - R{_1})}{(R{_2} - R{_1})}$R${_2}$$\Omega$